last modified: Friday, 21-May-2010 23:28:56 CEST
Document status: usable, some images missing
To describe the geometrical characteristics of a crystal, 5 terms are usually distinguished: crystal system, crystal class, habit, form, and twinning.
These notions are in turn all based on the concepts of the unit cell and the point lattice.
Unit Cell and Point Lattice
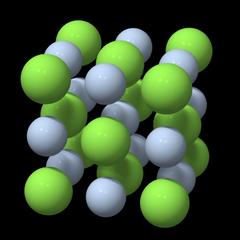
Fig. 1 |
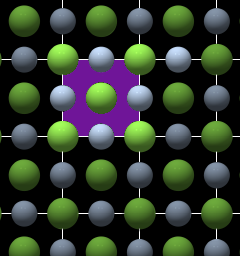
Fig. 2 |
Crystal System
The angles between the axes of the point lattice and the relative length of the edges of the unit cell are used to define various crystal systems. Every mineral (except those that are amorphous) belongs to one of the 7 crystal systems (or 6, as sometimes the rhombohedral/trigonal and the hexagonal system are grouped together). The following table gives a short overview.
| Angles | Axes | Crystal System |
|---|---|---|
| α = β = γ = 90° | a = b = c | Cubic or Isometric |
| α = β = γ = 90° | a = b , c ≠ a , c ≠ b | Tetragonal |
| α = β = γ = 90° | a ≠ b ≠ c | Orthorhombic |
| α = β = γ ≠ 90° | a = b = c | Trigonal or Rhombohedral |
| α = β = 90° , γ = 120° | a = b , c ≠ a , c ≠ b | Hexagonal |
| α ≠ β ≠ γ , β = 90° | a ≠ b ≠ c | Monoclinic |
| α ≠ β ≠ γ ≠ 90° | a ≠ b ≠ c | Triclinic |
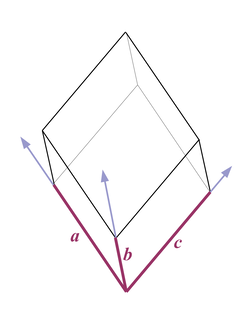 Fig. 3 |
A trigonal unit cell looks like an oblique cube - the lengths of all axes a, b, and c are equal, and the angles in the corresponding corners are equal but not rectangular (Fig. 3).
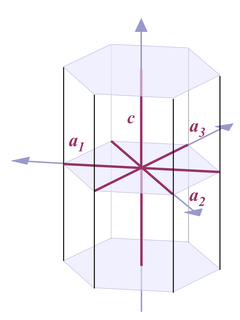 Fig. 4 |
Thus when it comes to describing quartz crystals, the terminology used is one for describing hexagonal crystals (Fig. 4):
Four axes are distinguished, a1, a2, a3, and c. All a axes are of equal length and lie in one plane, with 120° angles between them. When referring to all of them or one of them and it doesn't matter which one, people use the symbol a0 or simply a. The c axis runs perpendicular to a0. Its length is different from the a axes, for quartz it's 1.100 times the length of a0.
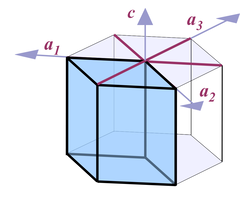 Fig. 5 |
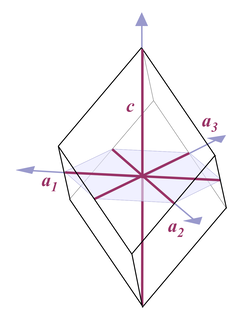 Fig. 6 |
Crystal or Symmetry Class
The term "crystal class" refers to the rotation and inversion symmetry properties of a mineral's crystal lattice. Every mineral (except those that are amorphous) belongs to one of the 32 symmetry classes.Quartz is member of the class 32, trigonal-trapezohedral - that reads "three - two", not thirty two. "32" is the so called Hermann-Maugin symbol, indicating that quartz has a 3-fold rotational symmetry on one and a two-fold rotational symmetry on another axis.
The notion of mirror symmetry is related to the notion of handedness or enantiomorphy. A unit cell can lack mirror symmetry: in that case, if you mirror the atomic coordinates around an axis, the positions do not match each other. Such a unit cell - and consequently the entire crystal - is either left- or right-handed, similar to our left and right hands.
Crystal Form
The term "crystal form" is a bit misleading, because it does not say anything about the actual shape of the crystal as a whole. A crystal form is a virtual geometrical body that is enclosed by lattice planes with identical symmetry properties.
 Fig. 7 |
 Fig. 8 |
All faces of a crystal form in a three-dimensional grid have the same shape, they are, for example, all squares or triangles. In certain crystal classes some forms are not "complete" bodies, but open at one or two ends, and are called open forms (e.g. all prisms), as opposed to the complete ones, which are called closed forms, a cube being an example [6].
The actual shape of a crystal can be viewed as a combination of intersecting forms. The shape thus depends both on presence and size of the different crystal forms. Crystals that look very different (e.g. one being elongated and the other short-prismatic) can still show the same crystal forms.
Because of this relation, the term "crystal form" also sometimes refers to the types of crystal faces that are visible on a crystal. Crystals with different types of crystals present on them are said to have a different form[7].
 Fig. 9 |
A form that is not stable in rock salt may very well be stable in other minerals of the cubic crystal system that have a different internal structure, like fluorite or garnet. Some minerals prefer to wear the same clothes every day, like rock salt, others show an astounding variety of forms and shapes that vary with the growth conditions, like pyrite, fluorite or, with about 200 different forms and more than 1000 known combinations, calcite.
There is a mathematical terminology for describing crystallographic forms, the so called Miller indices for crystal systems with three axes and the extension for crystal systems with four axes, the Miller-Bravais indices. The vector annotation used in this terminology (for example, {1 0 1 1} for the positive rhombohedral form r in quartz) exactly describes the relation of forms to the underlying crystal lattice. An introductory explanation of this awkward nomenclature is in preparation, but meanwhile I have to direct you to other websites and to textbooks of mineralogy to get into this rather complex and abstract topic:
Twinning
 Fig. 10 |
With respect to the crystal lattice, two kinds of geometrical operations can be performed to get a twinned crystal:
So each twinning law is defined by the kind of geometrical operation and the specific crystallographic plane or axis. The twinning axes and planes do not have to coincide with the main crystallographic axes.
One further distinguishes penetration twins and contact twins:
Contrary to common belief the terms contact twin and penetration twin do not define if subindividuals are macroscopically visible or not.
In theory, there are almost as many different twinning laws as crystal forms, but in nature only very few can actually be observed in a mineral species. Quartz, for instance, only three types of twins are frequently found.
Parallelly intergrown crystals might look like twins to most people, but in most cases they are not twins.
Note:
Again, I would recommend the very nice explanation that can be found at this website: Introduction to Crystallography and Mineral Crystal Systems.
2
Although when René Just Haüy came up with the idea of the unit cell in 1784, he did indeed think of unit cells as fundamental bricks that form a crystal.
3
Usually 3 axes, but the hexagonal unit cell is an exception, it has 4 axes forming a three-dimensional grid.
4
Some authors put quartz into the hexagonal crystal system. There is nothing wrong with that, it′s just that they choose to distinguish 6 crystal systems and regard the trigonal system as a special case of the hexagonal system. The unit cell of quartz is not trigonal, but hexagonal.
5
To demonstrate it in a quartz lattice is very confusing because the structure is very complex and for the same reason beyond my technical possibilities.
6
A form does not have to be a three-dimensional body, it can be a simple two-dimensional plane.
7
In German there is an appropriate term for the fact that two crystals show equivalent crystal faces: they are said to have the same "Tracht", which is an old-fashioned expression for clothing. There is probably also a corresponding expression in English that I don′t know.
Copyright © 2005-2013, A.C. A k h a v a n
Impressum
- Source: http://www.quartzpage.de/crs_terms.html
Note that even if the twin has a twinning axis and not a twinning plane, it still has a composition plane.
Crystal Habit
"Crystal habit" refers to the overall shape of the crystal, leaving aside its inner structure.
The crystal habit can be described in obvious terms like "barrel-like", "needle-like", "elongated", or "short-prismatic".
However, the notion of crystal habit also includes less obvious terms as "trigonal habit" or terms which are specific to individual minerals, like "Dauphiné habit". The habit of a crystal is dependent on the relative sizes of crystal faces. For example, the dominance of certain forms on a quartz crystal might cause a cube-like look that is accordingly called "pseudo-cubic habit".
One can also use the term "habit" to describe the general appearance of mineral aggregates, as opposed to a single crystal. Typical terms in that context are "druzy", "compact", "dendritic", "fibrous", or "granular".
Further Information, Literature, Links
Any textbook on mineralogy will discuss this topic extensively.
Footnotes
1
There is no distance between the atoms, but to visualize their geometric relationship, I′ve left some space between them. If one could actually see the atoms, they would perhaps look more like a cloudy sphere with no clear border or surface, the clouds consisting of quickly moving electrons.
 Printer Friendly Version
Printer Friendly Version
